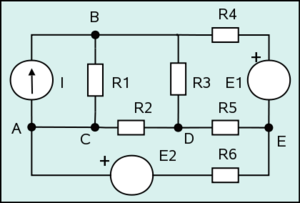
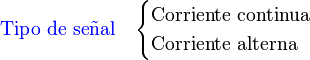En electrodinámica un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina (inductancia) y un condensador (capacidad).

Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describen generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primero orden).

Con ayuda de un generador de señales, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento del corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencia que lo rige).

Circuitos RLC

En los circuitos RLC se acoplan resistencias, capacitores e inductores. Existe también un ángulo de desfasaje entre las tensiones y corrientes (y entre las potencias), que incluso puede llegar a hacerse cero. En caso de que las reactancias capacitivas e inductivas sean de distinto valor para determinada frecuencia, tendremos desfasajes.

Dependiendo de cual de las reactancias sea mayor podremos afirmar si se trata de un circuito con características capacitivas o inductivas y por lo tanto si la tensión adelanta a la corriente (y con qué ángulo) o si la corriente adelanta a la tensión.

A continuación detallamos los valores de un circuito RLC simple en serie.

                                


Reactancia capacitiva


ω = Velocidad angular = 2πf
C = Capacidad
Xc = Reactancia capacitiva


Reactancia inductiva



ω = Velocidad angular = 2πf
L = Inductancia
Xl = Impedancia inductiva

Impedancia total del circuito RLC serie



R = Resistencia
Xl = Reactancia inductiva
Xc = Reactancia capacitiva

Angulo de desfasaje entre tensión y corriente



Xl = Reactancia inductiva
Xc = Reactancia capacitiva
R = Resistencia


Corriente máxima
El módulo de la corriente máxima que circula por el circuito es igual al módulo de la tensión máxima sobre el módulo de la impedancia.



Corriente eficaz
Para ondas senoidales podemos calcular la intensidad eficaz como:

CIRCUITOS RC

CIRCUITOS RC

Un circuito RC es un circuito compuesto de resistores y condensadores alimentados por una fuente eléctrica. Un circuito RC de primer orden está compuesto de un resistor y un condensador y es la forma más simple de un circuito RC. Los circuitos RC pueden usarse para filtrar una señal, al bloquear ciertas frecuencias y dejar pasar otras. Los filtros RC más comunes son el filtro paso alto, filtro paso bajo, filtro paso banda, y el filtro elimina banda. Entre las características de los circuitos RC está la propiedad de ser sistemas lineales e invariantes en el tiempo; reciben el nombre de filtros debido a que son capaces de filtrar señales eléctricas de acuerdo a su frecuencia.

En la configuración de paso bajo el condensador está en serie a la señal de salida del circuito primero la resistencia, después el condensador; mientras que en la configuración de paso alto el condensador cambia lugar con la resistencia.

Este mismo circuito tiene además una utilidad de regulación de tensión, y en tal caso se encuentran configuraciones en paralelo de ambos, la resistencia y el condensador, o alternativamente, como limitador de subidas y bajas bruscas de tensión con una configuración de ambos componentes en serie. Un ejemplo de esto es el circuito Snubber.

                                                

En un circuito RC en serie lacorriente (corriente alterna) que pasa por la resistor y por el capacitor es la misma

El voltaje VS es igual a la suma fasorial del voltaje en el resistor (Vr) y el voltaje en el capacitor (Vc).

Pero algo diferente pasa con los voltajes. En el resistor, el voltaje y la corriente están en fase (sus valores máximos y mínimos coinciden en el tiempo). Pero el voltaje en el capacitor no es así.
Como el capacitor se opone a cambios bruscos de voltaje, el voltaje en el capacitor está retrasado con respecto a la corriente que pasa por él. (el valor máximo de voltaje en el capacitor sucede después del valor máximo de corriente en 90^o).
Estos 90º equivalen a ¼ de la longitud de onda dada por la frecuencia de la corriente que está pasando por el circuito.


El voltaje total que alimenta elcircuito RC en serie es igual a la suma fasorial del voltaje en el resistory el voltaje en el capacitor.

Este voltaje tiene un ángulo de desfase (causado por el capacitor) y se obtiene con ayuda de las siguientes fórmulas:

Valor del voltaje (magnitud): Vs = ( VR² + VC² )^1/2
Angulo de desfase Θ =  Arctang (-VC/VR)

circuitos rl

Los circuitos RL son aquellos que contienen una bobina (inductor) que tiene autoinductancia, esto quiere decir que evita cambios instantáneos en la corriente. Siempre se desprecia la autoinductancia en el resto del circuito puesto que se considera mucho menor a la del inductor

                                             

Para un tiempo igual a cero, la corriente comenzará a crecer y el inductor producirá igualmente una fuerza electromotriz en sentido contrario, lo cual hará que la corriente no aumente. A esto se le conoce como fuerza contraelectromotriz.

Esta fem está dada por:  V = -L (inductancia) dI/dt

Debido a que la corriente aumentará con el tiempo, el cambio será positivo (dI/dt) y la tensión será negativa al haber una caída de la misma en el inductor.

Según kirchhoff:                     V = (IR) + [L (dI /  dt)]

         IR = Caída de voltaje a través de la resistencia.

Esta es una ecuación diferencial y se puede hacer la sustitución:

               x = (V/R) – I           es decir;       dx = -dI

Sustituyendo en la ecuación:     x + [(L/R)(dx/dt)] = 0      dx/x = - (R/L) dt

Integrando:                                  ln (x/xo) = -(R/L) t

Despejando x:                               x = xo e ^{–Rt / L}

Debido a que                                     xo = V/R

El tiempo es cero , y corriente cero              V/R – I = V/R e ^{–Rt / L}

                                 I = (V/R) (1 - e ^{–Rt / L})

El tiempo  del circuito está representado por  t = L/R

                                 I = (V/R) (1 – e ^{– 1/}t)

 Donde para un tiempo infinito, la corriente de la malla será  I = V/R. Y se puede considerar entonces el cambio de la corriente en el tiempo como cero.

Para verificar la ecuación que implica a t y a I, se deriva una vez y se reemplaza en la inicial:                                  dI/dt = V/L e ^{– 1/}t

 Se sustituye:                             V = (IR) + [L (dI /  dt)] 

V = [ (V/R) (1 – e ^{– 1/}t)R + (L V/ L e ^{– 1/}t)]

 V – V e ^{– 1/}t = V – V e ^{– 1/}t

OSCILACIONES EN UN CIRCUITO LC

Cuando un condensador se conecta a un inductor, tanto la corriente como la carga den el condensador oscila. Cuando existe una resistencia, hay una disipación de energía en el sistema porque una cuanta se convierte en calor en la resistencia, por lo tanto las oscilaciones son amortiguadas. Por el momento, se ignorará la resistencia.

                                                             

En un tiempo igual a cero, la carga en el condensador es máxima y la energía almacenada en el campo eléctrico entre las placas es U = Q²máx/(2C). Después de un tiempo igual a cero, la corriente en el circuito comienza a aumentar y parte de la energía en el condensador se transfiere al inductor. Cuando la carga almacenada en el condensador es cero, la corriente es máxima y toda la energía está almacenada en el campo eléctrico del inductor. Este proceso se repite de forma inversa y así comienza a oscilar.

En un tiempo determinado, la energía total del sistema es igual a la suma de las dos energías (inductor y condensador):  U = Uc + UL

 U = [ Q²/(2C) ] + ( LI²/2 )

circuitos eléctricos

circuitos eléctricos:

Un circuito es una red eléctrica (interconexión de dos o más componentes, tales como resistencias, inductores, condensadores, fuentes, interruptores y semiconductores) que contiene al menos una trayectoria cerrada. Los circuitos que contienen solo fuentes, componentes lineales (resistores, condensadores, inductores) y elementos de distribución lineales (líneas de transmisión o cables) pueden analizarse por métodos algebraicos para determinar su comportamiento en corriente directa o en corriente alterna. Un circuito que tiene componentes electrónicoses denominado un circuito electrónico. Estas redes son generalmente no lineales y requieren diseños y herramientas de análisis mucho más complejos.

Partes

Figura 1: circuito ejemplo.

• Componente: Un dispositivo con dos o más terminales en el que puede fluir interiormente una carga. En la figura 1 se ven 9 componentes entre resistores y fuentes.
• Nodo: Punto de un circuito donde concurren más de dos conductores. A, B, D, E son nodos. Nótese que C no es considerado como un nuevo nodo, puesto que se puede considerar como un mismo nodo en A, ya que entre ellos no existe diferencia de potencial o tener tensión 0 (V_A - V_C = 0).
• Rama: Conjunto de todos los elementos de un circuito comprendidos entre dos nodos consecutivos. En la figura 1 se hallan siete ramales: AB por la fuente, BC por R1, AD, AE, BD, BE y DE. Obviamente, por un ramal sólo puede circular una corriente.
• Malla: Cualquier camino cerrado en un circuito eléctrico.
• Fuente: Componente que se encarga de transformar algún tipo de energía en energía eléctrica. En el circuito de la figura 1 hay tres fuentes: una de intensidad, I, y dos de tensión, E1 y E2.
• Conductor: Comúnmente llamado cable; es un hilo de resistencia despreciable (idealmente cero) que une los elementos para formar el circuito.

• Clasificación

  Los circuitos eléctricos se clasifican de la siguiente forma:

  

  

  

  

MALLAS Y NODOS:

Nodos, Supernodos, Malla y Supermalla

Análisis de nodos
                                              

Figura 1: La ley de corrientes de Kirchhoff es la base del análisis de nodos.

En análisis de circuitos eléctricos, el análisis de nodos, o método de tensiones nodales es un método para determinar la tensión (diferencia de potencial) de uno o más nodos.

Cuando se analiza un circuito por las leyes de Kirchhoff, se podrían usar análisis de nodos (tensiones nodales) por la ley de corrientes de Kirchhoff (LCK) o análisis de malla (corrientes de malla) usando la ley de tensiones de Kirchhoff (LVK). En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero en cualquier instante, por lo que una carga    nunca puede acumularse en un nodo. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito. Así, en cada relación se debe dar la corriente en función de la tensión que es nuestra incógnita, por la conductancia. Por ejemplo, para un resistor, 

Irama = Vrama * G, donde G es la Conductancia del resistor.

El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones, que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente usando álgebra lineal en un computador. Por el hecho de que forme ecuaciones muy sencillas, este método es una base para muchos programas de simulación de circuitos (Por ejemplo, SPICE). Cuando los elementos del circuito no tienen conductancia, se puede usar una extensión más general del análisis de nodos, El análisis de nodos modificado.

Los ejemplos simples de análisis de nodos se enfocan en elementos lineales. Las redes no lineales (que son más complejas) también se pueden resolver por el análisis de nodos al usar el método de Newton para convertir el problema no lineal en una secuencia de problemas lineales.

 

Procedimiento

 

Figura 2: Se elige el nodo con más conexiones como nodo de referencia (cuya tensión es 0) y se asignan 3 variables Va, Vb y Vc

1.    Localice los segmentos de cable conectados al circuito. Estos serán los nodos que se usarán para el método.

2.    Seleccione un nodo de referencia (polo a tierra). Se puede elegir cualquier nodo ya que esto no afecta para nada los cálculos; pero elegir el nodo con más conexiones podría simplificar el análisis.

3.    Identifique los nodos que están conectados a fuentes de voltaje que tengan una terminal en el nodo de referencia. En estos nodos la fuente define la tensión del nodo. Si la fuente es independiente, la tensión del nodo es conocida. En estos nodos no se aplica la LCK.

4.    Asigne una variable para los nodos que tengan tensiones desconocidas. Si la tensión del nodo ya se conoce, no es necesario asignarle una variable. (Véase Figura 2)

5.    Para cada uno de los nodos, se plantean las ecuaciones de acuerdo con las Leyes de Kirchhoff. Básicamente, sume todas las corrientes que pasan por el nodo e igualelas a 0. Si el número de nodos es n, el número de ecuaciones será por lo menos n − 1 porque siempre se escoge un nodo de referencia el cual no se le elabora ecuación.

6.    Si hay fuentes de tensión entre dos tensiones desconocidas, una esos dos nodos como un supernodo. Las corrientes de los dos nodos se combinan en una nueva ecuación muy sencilla.

7.    Resuelva el sistema de ecuaciones simultáneas para cada tensión desconocida.

Ejemplos

   Ejemplo 1: Caso básico

 

Figura 3: Circuito sencillo con una tensión desconocida V1.